FPGA中乘法器的加速运算

发表于 阅读次数： 阅读次数： 本文字数： 8.7k 阅读时长 ≈ 16 分钟

数字逻辑与系统设计设计报告

项目内容

题目：8位乘法器\
实现的功能:

  • 输入为两个8位有符号数或无符号数，输出16位相乘结果
  • 采用Booth算法对乘法转化为部分和求和
  • 采用Wallace算法减少部分和求和时所使用的全加器数量

编译器及测试仿真环境

win11系统，EDA环境为Quartus，EDA软件版本为18.0，验证板卡为DE10Lite，波形仿真软件为Modelsim，软件版本为SE-64 2020.4

该8位乘法器设计特点

本文采用Radix-4 Booth乘法器对乘法运算化简为4个部分和求和；同时对化简后的部分和采用Wallace树算法进行加速运算，减少全加器和半加器数量的使用。

Radix-4 Booth算法

Booth算法原理:

对于8位有符号数A可以表示为如(1)式所示，其中用$A_{i}$表示A的第$i$位:

同时考虑对$A_{i}$进行如下分解:

进而可以对8位有符号数A进行如下分解，补充定义$A_{-1}=0$得:

因此$A\times B$可表示如下式所示:

可以发现$2^{i},i=0,2,4,6$前的系数是由$A_{i},A_{i+1},A_{i+1}$构成的形式相近的式子，不妨记为$Coef$，故$Coef$与$A_{i}$,$A_{i+1}$,$A_{i+1}$满足的关系如下表所示:

$A_{i+1}$ $A_{i}$ $A_{i-1}$ $Coef$
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 2
1 0 0 -2
1 0 1 -1
1 1 0 -1
1 1 1 0

故可以将两个8位有符号数A,B的乘积$A\times B$转变为4个部分和的形式，实现计算量和资源使用量的减少。同时$Coef$的系数是有限的，故我们可以将$Coef$对应的操作按如下方式使用寄存器提前存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
p <= 16'd0;
// 完成 M 的位扩展，为防止 2M 溢出，因此扩展到 16 位
M <= {{8{multiplicand[7]}},multiplicand};
// 完成 -M 的位扩展，为防止 -2M 溢出，因此扩展到 16 位
M_shadow <= {{8{~multiplicand[7]}},~multiplicand+1'b1};
// 完成 2M 的位扩展，为防止 2M 溢出，因此扩展到 16 位
M2 <= {{8{multiplicand[7]}}, multiplicand << 1};
// 完成 -2M 的位扩展，为防止 -2M 溢出，因此扩展到 16 位
M2_shadow <= {{8{~multiplicand[7]}}, (~multiplicand+1'b1) << 1};
// N 来选择 booth 的操作，因此用来寄存乘数的值，最后补一个 0，相当于y_{-1}
N <= {multiplier,1'b0};
shift_num <= 4'd0;
i <= i + 1'b1;

同时定义RSTn和done信号用于表征乘法运算的开始和结束，同时利用case语句实现对4个部分和的逐次表征，并利用多个$if$语句实现对$Coef$的判断进而实现对部分和形式的确定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
module booth_multiply#(
    parameter DATAWIDTH = 8//定义符号数宽度为8bit
)
(
    input                            CLK,//定义系统时钟
    input                            RSTn,//定义复位信号RSTn
    input                            START,//定义乘法器工作开启信号，拉低时有效
    input  [ DATAWIDTH - 1 : 0 ]     A,//定义multiplier
    input  [ DATAWIDTH - 1 : 0 ]     B,//定义multiplicand

    output [ DATAWIDTH * 2 - 1 : 0 ] RESULT,//定义product
    output                           Done//定义乘法器工作结束信号，拉高时有效
);

reg [ DATAWIDTH - 1 : 0 ] i;
reg [ DATAWIDTH * 2 : 0 ] P;
reg [ DATAWIDTH - 1 : 0 ] A_reg;
reg [ DATAWIDTH - 1 : 0 ] A_bm;
reg [ DATAWIDTH - 1 : 0 ] N;
reg [ DATAWIDTH * 2 : 0 ] result_reg;
reg                       isDone;

always @ ( posedge CLK or negedge RSTn )
begin
    if (!RSTn)
    begin
        i <= 0;
        P <= 0;
        A_reg <= 0;
        A_bm <= 0;
        result_reg <= 0;
        N <=0;
        isDone <= 0;
    end
		else if (START)
    begin
        case (i)

        0:begin
          A_reg <= A;//计算A的补码,方便后面的+-操作
          A_bm <= ~A + 1'b1;    
          P <= { 8'd0, B, 1'b0 };  //B add to last 8bit of P
          i <= i + 1'b1;
          N <= 0;
          end//operating 这一个状态用来判断最低两位，然后决定执行什么操作
        1:begin
          if (N == DATAWIDTH)
            begin
            N <= 0;
            i <= i + 2'b10;
            end
				else if (P[1:0] == 2'b00 | P[1:0] == 2'b11)
            begin
            P <= P;
            i <= i + 1'b1;
            end
				else if (P[1:0] == 2'b01)
            begin
            P <= {P[16:9] + A_reg,P[8:0]};
            i <= i + 1'b1;
            end
				else if (P[1:0] == 2'b10)
            begin
            P <= {P[16:9] + A_bm,P[8:0]};
            i <= i + 1'b1;
            end
		  end
            //shift 这是无论最低两位是什么，最后都要执行的移位操作
        2:
          begin
          P <= {P[16],P[16:1]};
          N <= N + 1'b1;
          i <= i - 1'b1;
          end
        3:
          begin
          isDone <= 1;
          result_reg <= P;
          i <= i + 1'b1;
		  end
        4:
          begin
          isDone <= 0;
          i <= 0;
          end
		endcase
    end
end

assign Done = isDone;
assign RESULT = result_reg[16:1];

endmodule

仿真测试与波形查看

  • testbench代码撰写如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
//注若要完整运行所有结果，至少运行1400ns
`timescale  1ns / 1ps    

module tb_booth_multiply;

parameter PERIOD     = 10;//定义时钟周期
parameter DATAWIDTH  = 8;// 定义乘数和被乘数的位宽

// 定义输出信号为寄存器reg类型
reg   CLK                                  = 0 ;
reg   RSTn                                 = 0 ;
reg   START                                = 0 ;
reg   [ DATAWIDTH - 1 : 0 ]  A             = 0 ;
reg   [ DATAWIDTH - 1 : 0 ]  B             = 0 ;

// 定义输出信号为线网wire类型
wire  [ DATAWIDTH * 2 - 1 : 0 ]  RESULT    ;
wire  Done                                 ;


initial
begin
    forever #(PERIOD/2)  CLK=~CLK;//时钟周期没到一半时钟信号翻转一次
end

initial
begin
    #(PERIOD) RSTn  =  1;START = 1;
end

booth_multiply #(
    .DATAWIDTH ( DATAWIDTH ))
 u_booth_multiply (
    .CLK                     ( CLK                               ),
    .RSTn                    ( RSTn                              ),
    .START                   ( START                             ),
    .A                       ( A       [ DATAWIDTH - 1 : 0 ]     ),
    .B                       ( B       [ DATAWIDTH - 1 : 0 ]     ),

    .RESULT                  ( RESULT  [ DATAWIDTH * 2 - 1 : 0 ] ),
    .Done                    ( Done                              )
);

initial
begin
    A = 2;
    B = 4;//正确输出结果应为8
    #200
    A = 3;
    B = 5;//正确输出结果应为15
    #200
    A = -4;
    B = 6;//正确输出结果应为-24
    #200
    A = 123;
    B = -56;//正确输出结果应为-6888
    #200
    A = 99;
    B = 44;//正确输出结果应为4356
    #200
    A = -34;
    B = -66;//正确输出结果应为2244
    #200
    A = 23;
    B = 12;//正确输出结果应为276
    #200
    A = 111;
    B = 100;//正确输出结果应为11100
    #400
    $finish;

end

endmodule

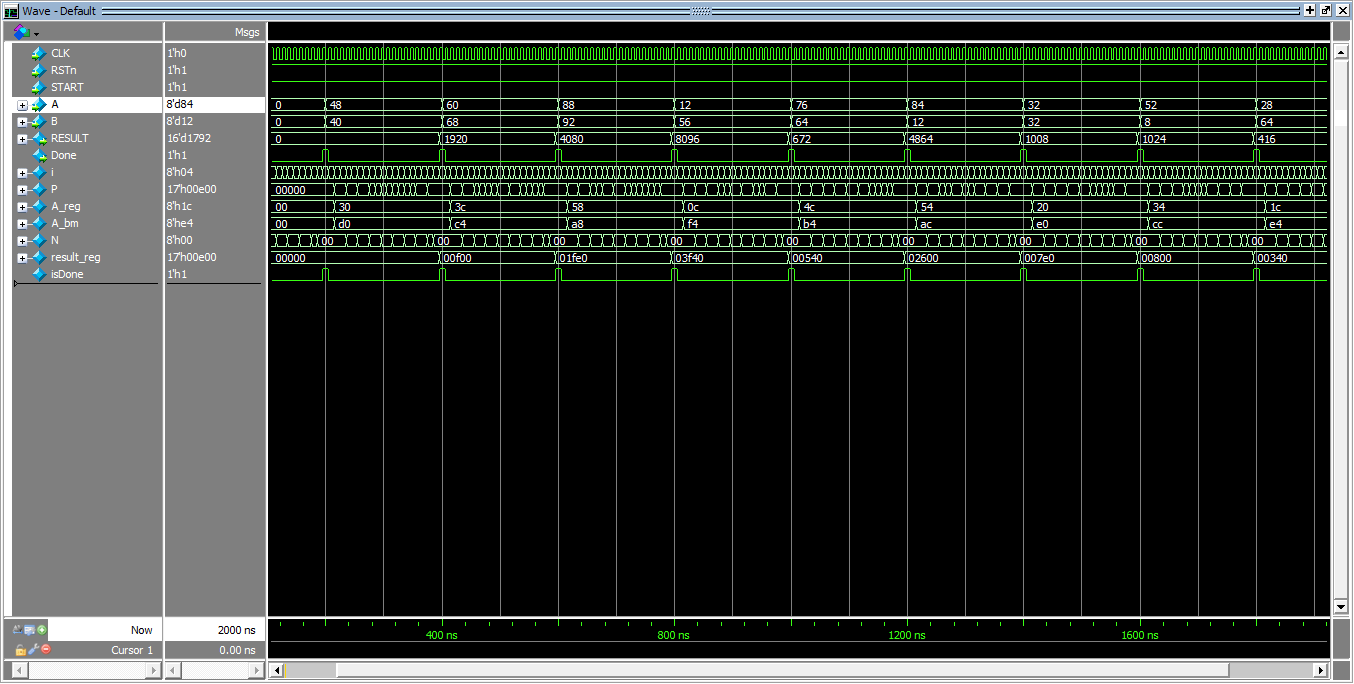
同时仿真波形如下图1所示:

图1 非随机数仿真波形

同时如果检测该乘法器对所有8位有符号数相乘的可行性，则上述在testbench中手动设置乘数和被乘数的方法则会过于麻烦，因此也可以考虑如下方法来设置随机数仿真。

  • 随机数型乘法器仿真testbench代码可补充如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
`timescale  1ns / 1ps    

module tb_booth_multiply;//random版

parameter PERIOD     = 10;//定义时钟周期
parameter DATAWIDTH  = 8;// 定义乘数和被乘数的位宽

// 定义输出信号为寄存器reg类型
reg   CLK                                  = 0 ;
reg   RSTn                                 = 0 ;
reg   START                                = 0 ;
reg   [ DATAWIDTH - 1 : 0 ]  A             = 0 ;
reg   [ DATAWIDTH - 1 : 0 ]  B             = 0 ;

// 定义输出信号为线网wire类型
wire  [ DATAWIDTH * 2 - 1 : 0 ]  RESULT    ;
wire  Done                                 ;


initial
begin
    forever #(PERIOD/2)  CLK=~CLK;//时钟周期没到一半时钟信号翻转一次
end

initial
begin
    #(PERIOD) RSTn  =  1;START = 1;
end

booth_multiply #(
    .DATAWIDTH ( DATAWIDTH ))
 u_booth_multiply (
    .CLK                     ( CLK                               ),
    .RSTn                    ( RSTn                              ),
    .START                   ( START                             ),
    .A                       ( A       [ DATAWIDTH - 1 : 0 ]     ),
    .B                       ( B       [ DATAWIDTH - 1 : 0 ]     ),

    .RESULT                  ( RESULT  [ DATAWIDTH * 2 - 1 : 0 ] ),
    .Done                    ( Done                              )
);

initial
begin
    A = 2;
    B = 4;//正确输出结果应为8
    #200
    A = 3;
    B = 5;//正确输出结果应为15
    #200
    A = -4;
    B = 6;//正确输出结果应为-24
    #200
    A = 123;
    B = -56;//正确输出结果应为-6888
    #200
    A = 99;
    B = 44;//正确输出结果应为4356
    #200
    A = -34;
    B = -66;//正确输出结果应为2244
    #200
    A = 23;
    B = 12;//正确输出结果应为276
    #200
    A = 111;
    B = 100;//正确输出结果应为11100
    #400
    $finish;
end
endmodule

但verilog中的随机数生成依赖于其中的种子seed，故我们可以直接利用乘数A的值做为下一次random生成所需的种子，这样我们就可以不用每次仿真调整随机数了，为我们测试乘法器的可靠性和鲁棒性带来方便。即将initial begin里的语句改成如下所示即可:

1
2
3
4
5
6
7
8
9
initial begin
	A = 0;
	B = 0;
	repeat(10) begin
		#200 A = {$random(A)}%100;
		B = {$random(A-1)}%100;
	end
	#5 $finish;
end

同时仿真波形如下图2-图3所示:

图2 随机数seed=1时仿真波形

图3 随机数seed=A时仿真波形

Wallace算法

本文采用Wallace算法实现对8位无符号数乘法器的加速，实现了部分和求和时所使用的全加器数量的减少。

全加器与半加器：全加器是一个三输入两输出的逻辑单元，它可以同时处理两个数据输入位以及一个来自前一级的进位输入，并产生一个本级的和输出以及一个向后一级传递的进位输出。而半加器仅处理两个数据输入位而不考虑前一级的进位，因此它的结构相对简单。

对于8位无符号数相乘，会出现8个部分积，故我们采用4:2压缩器，将其先压缩为4个部分积，再压缩为2个部分积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//定义16位部分积的4:2压缩器
module wallace(x, y, out);
parameter size = 8; // 定义参数，乘法器的位数(8位无符号数)
input [size-1:0] x, y; // 输入y是乘数，x是被乘数
output [2*size-1:0] out;

wire [size*size-1:0] a; // a为部分积
wire [1:0] b0, b1; // 第一级的输出，包含进位
wire [1:0] c0, c1, c2, c3; // 第二级的输出，包含进位
wire [5:0] add_a, add_b; // 第三级的输入
wire [6:0] add_out; // 第三级的输出

wire [2*size-1:0] out; // 乘法器的输出（组合逻辑）

assign a = {x[3], x[2], x[3], x[1], x[2], x[3], x[0], x[1],x[2], x[3], x[0], x[1], x[2], x[0], x[1], x[0]}
& {y[3], y[3], y[2], y[3], y[2], y[1], y[3], y[2],y[1], y[0], y[2], y[1], y[0], y[1], y[0], y[0]}; // 部分积

// 4:2压缩器
module compressor4_2(i1,i2,i3,i4,cin,c_out,C,S)
input i1,i2,i3,i4,cin;
output C,S;

wire s_temp;
assign {cout,s_temp} = i1+i2+i3;//4:2压缩器中的第一级全加器
assign {C,S} = cin+s_temp+i4;//4:2压缩器中的第二级全加器

endmodule

module pp_compressor4_2(
input [15:0] pp_in1,
input [15:0] pp_in2,
input [15:0] pp_in3,
input [15:0] pp_in4,
output [15:0] C,
output [15:0] S
);

wire[15:0] C_comb;
wire[15:0] S_comb;
wire[15:0] C_temp;
wire[16:0] C_temp_append_0;

assign C_temp_append_0 = {C_temp,1'b0};//[0]位的进位Cin为1'b0;

genvar i;
generate 
    for(i=0;i<16;i=i+1)
    begin:compressor4_2_inst
        compressor4_2 u_compressor4_2(
            .i1(pp_in1[i]),
            .i2(pp_in2[i]),
            .i3(pp_in3[i]),
            .i4(pp_in4[i]),
            .cin(C_temp_append_0[i]),
            .cout(C_temp_append_0[i+1]),
            .C(C_comb[i]),
            .S(S_comb[i])
        );
    end
endgenerate

assign S=S_comb;
assign C={C_comb[14:0],1'b0};//进位C比Sum高一位，故左移一位

endmodule

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
module(
input[7:0] a,
input[7:0] b,
output[15:0] S
);

wire[15:0] partial_res0;
wire[15:0] partial_res1;
wire[15:0] partial_res2;
wire[15:0] partial_res3;
wire[15:0] partial_res4;
wire[15:0] partial_res5;
wire[15:0] partial_res6;
wire[15:0] partial_res7;

wire[15:0] C1;
wire[15:0] C2;
wire[15:0] C3;
wire[15:0] S1;
wire[15:0] S2;
wire[15:0] S3;

//计算8个16位部分积
assign partial_res0={8'b0,b*a[0]};
assign partial_res1={7'b0,b*a[1],1'b0};
assign partial_res2={6'b0,b*a[2],2'b0};
assign partial_res3={5'b0,b*a[3],3'b0};
assign partial_res4={4'b0,b*a[4],4'b0};
assign partial_res5={3'b0,b*a[5],5'b0};
assign partial_res6={2'b0,b*a[6],6'b0};
assign partial_res7={1'b0,b*a[7],7'b0};

//第一次压缩，将8个部分积压缩为4个部分积
pp_compressor4_2 u1(partial_res0,partial_res1,partial_res2,partial_res3,C1,S1);
pp_compressor4_2 u2(partial_res4,partial_res5,partial_res6,partial_res7,C2,S2);

//第二次压缩，将4个部分积压缩为2个部分积
pp_compressor4_2 u3(C1,S1,C2,S2,C3,S3);

//计算最终结果
assign S = C3+S3;