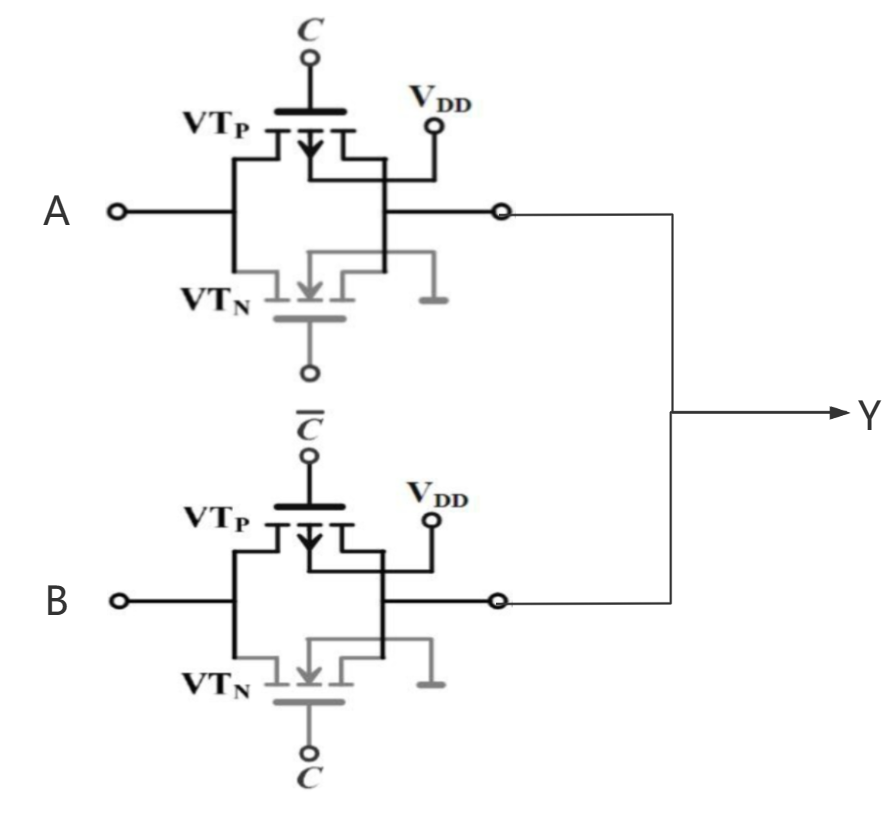
利用传输门做二选一选择器的CMOS电路分析

祝老师教师节快乐！暨利用传输门做二选一选择器的CMOS电路分析

祝天下的老师们教师节快乐！祝老师工作顺利，万事如意！

利用传输门做二选一选择器的CMOS电路分析

灵感来源于今天的数字逻辑课程，因为对学数电时的传输门的印象不清了，然后分析传输门的CMOS电路时绕晕了，故做此记录。

注：分析传输门的CMOS电路时，不需要关注MOS管是否工作在饱和区，只需关注导电沟道是否产生即可。

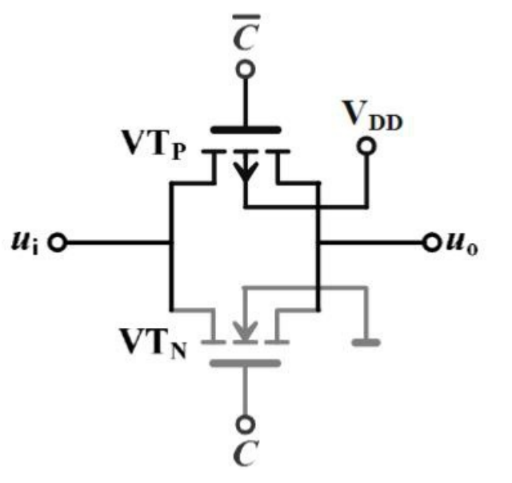
如图1所示为传输门的CMOS电路示意图

• 当 $C=1$ 时，下面对MOS管的导通情况进行分析:

NMOS导通情况

$$\begin{align*} \because &C=1\\ \therefore &V_{GN} = V_{DD} \\ \because &V_{BN} = 0V\\ \end{align*}$$ $$\begin{align*} \therefore &V_{GSN} = V_{GBN} -V_{SBN} = V_{DD} - V_{i} \end{align*}$$

PMOS导通情况

$$\begin{align*} \because &\overline{C}=0\\ \therefore &V_{GP} = 0V \\ \because &V_{BP} = V_{DD}\\ \end{align*}$$ $$\begin{align*} \therefore &V_{GSP} = V_{GBP} - V_{SBP} = V_{DD} - (V_{i} - V_{DD}) = - V_{i} \end{align*}$$

当 $V_{i}<V_{DD}-V_{TH}$ ，可保证 $V_{GSN}=V_{DD}-V_{i}\geq v_{TH}$ ，即NMOS产生导电沟道；

当 $V_{i} > V_{TH} $ ，可保证 $V_{GSP}=-V_{i}\leq-v_{TH}$ ，即PMOS产生导电沟道；

故 $V_{i}$ 无论取任何值(但都必须保证小于 $V_{DD}$ )都可保证至少有一个MOS管存在导电沟道，使得 $V_{o}=V_{i}$ 。

• 当 $C=0$ 时，下面对MOS管的导通情况进行分析:

NMOS导通情况

$$\begin{align*} \because &C=1\\ \therefore &V_{GN} = 0V \\ \because &V_{BN} = 0V\\ \end{align*}$$ $$\begin{align*} \therefore &V_{GSN} = 0 < V_{TH} \end{align*}$$

PMOS导通情况

$$\begin{align*} \because &\overline{C}=1\\ \therefore &V_{GP} = V_{DD} \\ \because &V_{BP} = V_{DD}\\ \end{align*}$$ $$\begin{align*} \therefore &V_{GSP} > - V_{TH} \end{align*}$$

故 $V_{i}$ 无论取任何值(但都必须保证小于 $V_{DD}$ )都无法使任意一个MOS管存在导电沟道。

故根据传输门导通规律设计如下图所示的二选一数选器

如图2所示。